Sylvain Barré
Ancien élève de l'ENS Lyon (pormotion 1990), agrégation (reçu 11ème), thèse sous la direction d'Étienne Ghys. Depuis 1998, maître de conférence à l'UBS au laboratoire de maths LMBA
Enseignant-Chercheur


Ancien élève de l'ENS Lyon (pormotion 1990), agrégation (reçu 11ème), thèse sous la direction d'Étienne Ghys. Depuis 1998, maître de conférence à l'UBS au laboratoire de maths LMBA
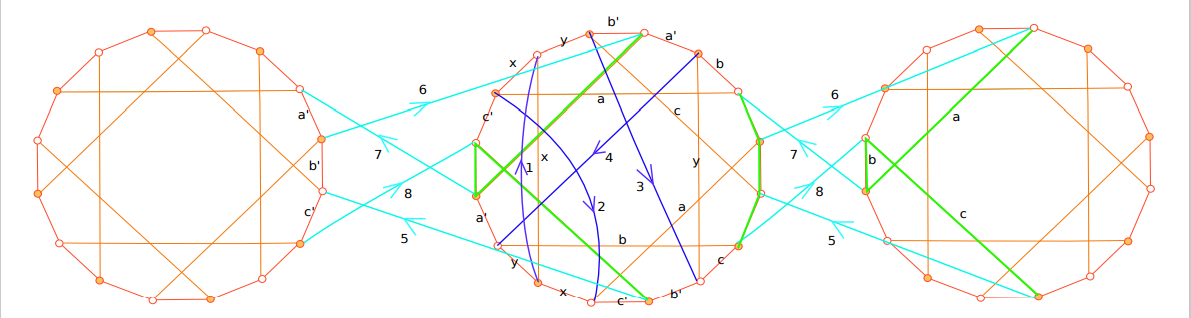
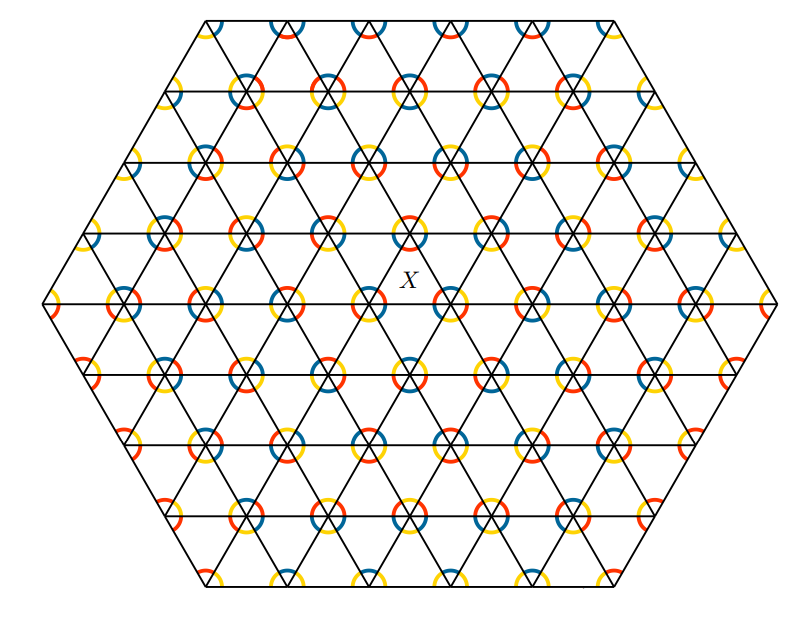
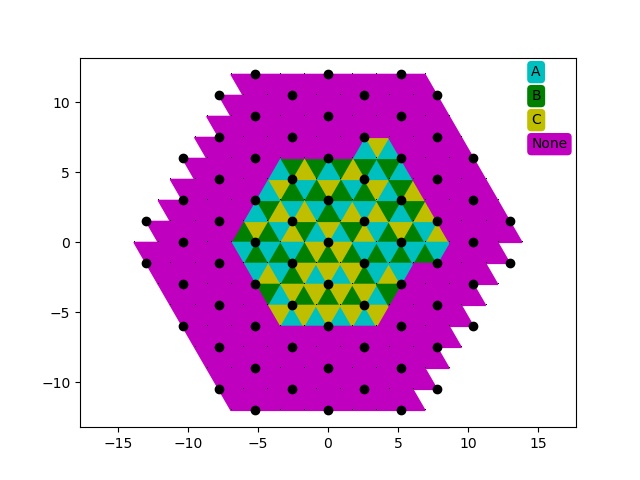
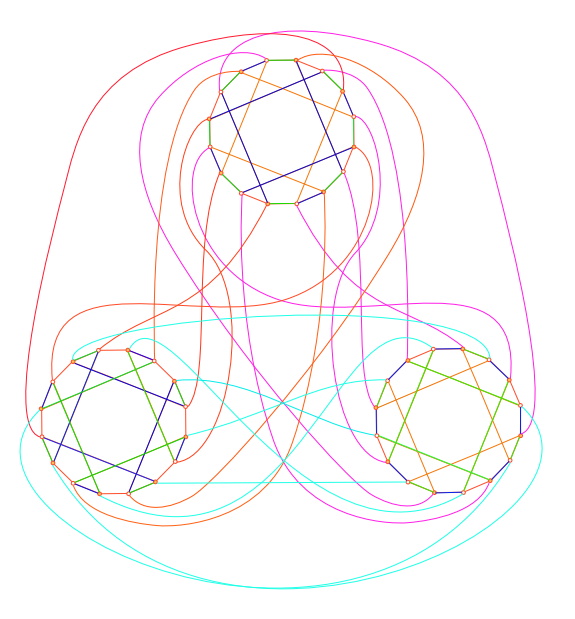
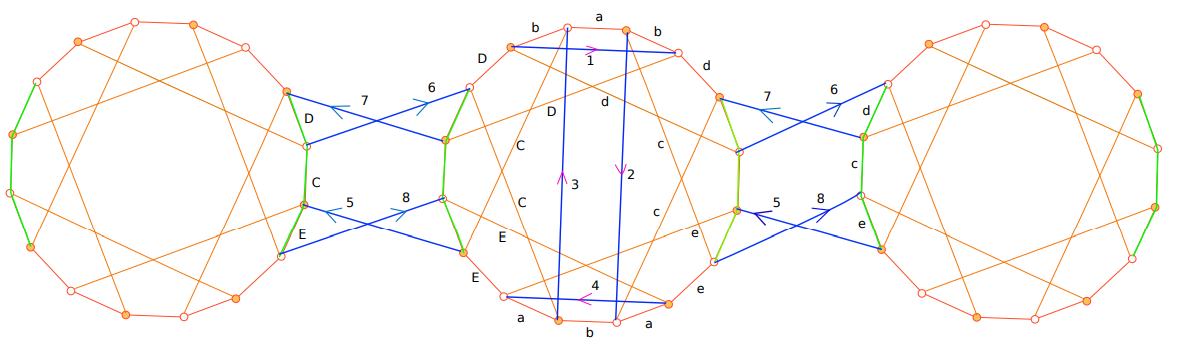
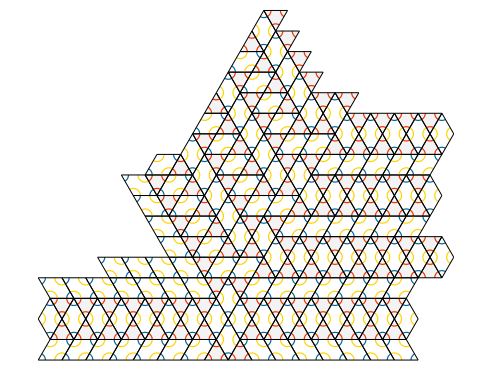
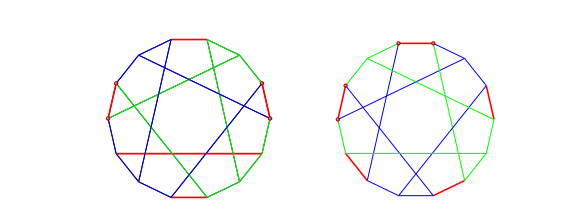
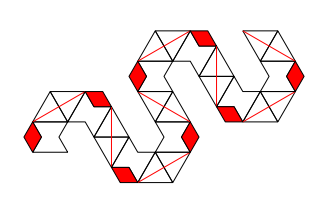
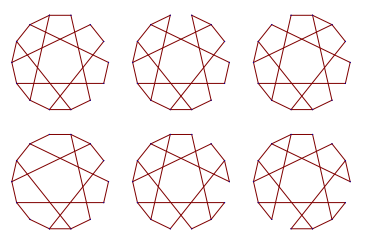
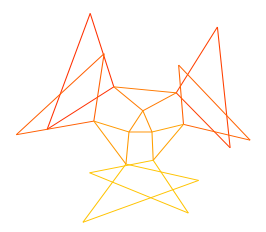
Sylvain Barré & Mikaël Pichot

Sylvain Barré & Mikaël Pichot
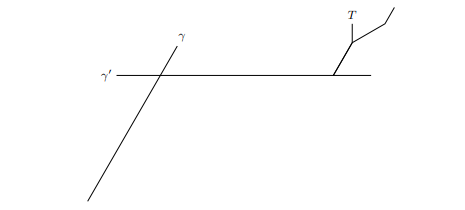
Sylvain Barré &Mikaël Pichot
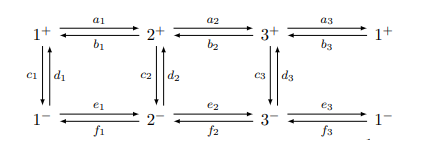
Sylvain Barré & Mikaël Pichot

Sylvain Barré & Mikaël Pichot

Sylvain Barré & Mikaël Pichot
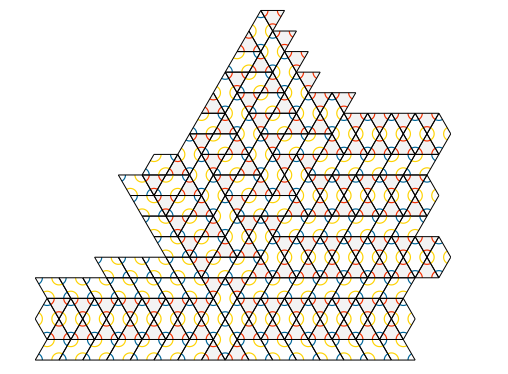
Sylvain Barré & Mikaël Pichot
Sylvain Barré & Mikaël Pichot
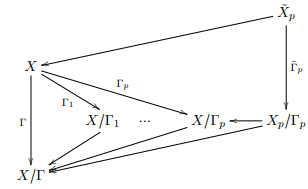
Sylvain Barré & Mikaël Pichot
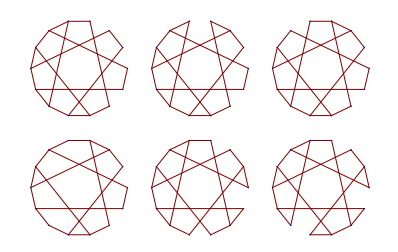
Sylvain Barré & Mikaël Pichot
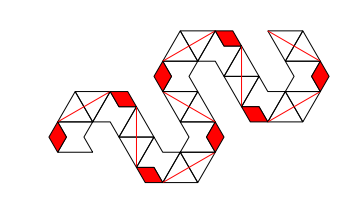
Sylvain Barré & Mikaël Pichot
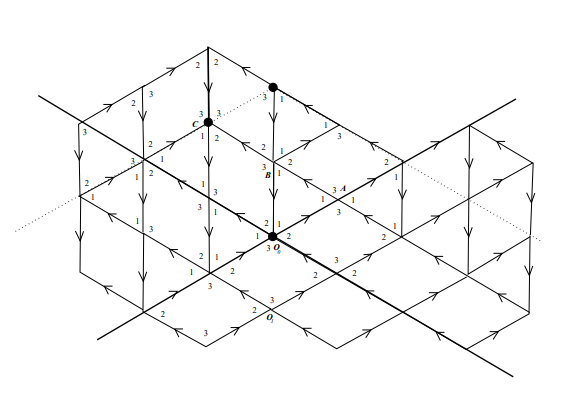
Sylvain Barré & Mikaël Pichot
Sylvain Barré & Mikaël Pichot
Sylvain Barré
Sylvain Barré
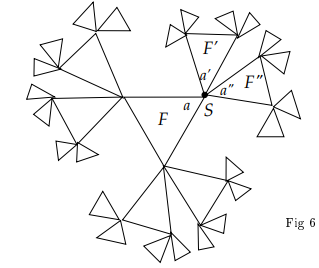
Sylvain Barré
Sylvain Barré
Sylvain Barré